4.7 KiB
Práctica 3
Práctica 3
Introducción
En esta práctica, usaremos distintos algoritmos de búsqueda, basados en trayectorias, para resolver el problema de la máxima diversidad (MDP). Implementaremos:
- Enfriamiento simulado
- Búsqueda multiarranque
Algoritmos
Enfriamiento simulado
El enfriamiento simulado es un algoritmo de búsqueda basado en trayectorias, con un criterio probabilístico basado en la termodinámica.
El procedimiento general del algoritmo queda ilustrado a continuación:
\begin{algorithm} \KwIn{A list $[a_i]$, $i=1, 2, \cdots, n$, that contains the components of a solution} \KwOut{Processed list} $currentSol \leftarrow initialize()$ $T0 \leftarrow initialize()$ $Tf \leftarrow initialize()$ $bestSol \leftarrow currentSol$ $T \leftarrow Tf$ \While{$T > Tf$}{ $neighbour \leftarrow generateNeighbour(currentSol)$ $delta \leftarrow fitness(neighbour) - fitness(currentSol)$ \If{$delta > 0 \vee acceptNeighbour(neighbour)$}{ $currentSol \leftarrow neighbour$ \If{$fitness(currentSol) > fitness(bestSol)$}{ $bestSol \leftarrow currentSol$ } } $coolDown(T)$ } \KwRet{$bestSolution$} \end{algorithm}Búsqueda multiarranque
La búsqueda multiarranque es un algoritmo que itera las 2 etapas siguientes:
- Generación de una solución inicial
- Búsqueda local
Es una variante simple de implementar a partir de una búsqueda local
El procedimiento general del algoritmo queda ilustrado a continuación:
\begin{algorithm} \KwIn{A list $[a_i]$, $i=1, 2, \cdots, m$, the solution} \KwOut{Processed list} $Solutions = [\ ]$ $initialSolutions \leftarrow getRandomSolutions()$ $Solutions.append(firstSolution)$ $maxIterations \leftarrow 1000$ \For{$i \leftarrow 0$ \KwTo $maxIterations$}{ \For{$element in initialSolutions$}{ $lastSolution \leftarrow getLastElement(initialSolutions)$ \While{$neighbour \leq lastSolution$}{ $neighbour \leftarrow getNeighbouringSolution(lastSolution)$ $Solutions.append(neighbour)$ $lastSolution \leftarrow getLastElement(neighbour)$ } $finalSolution \leftarrow getLastElement(Solutions)$ } } \KwRet{$finalSolution$} \end{algorithm}Implementación
La práctica ha sido implementada en Python, usando las siguientes bibliotecas:
- NumPy
- Pandas
\clearpage
Instalación
Para ejecutar el programa es preciso instalar Python, junto con las bibliotecas Pandas y NumPy.
Se proporciona el archivo shell.nix para facilitar la instalación de las dependencias, con el gestor de paquetes Nix. Tras instalar la herramienta Nix, únicamente habría que ejecutar el siguiente comando en la raíz del proyecto:
nix-shellEjecución
La ejecución del programa se realiza mediante el siguiente comando:
python src/main.py <dataset> <algoritmo>Los parámetros posibles son:
| dataset | algoritmo |
| Cualquier archivo de la carpeta data | annealing |
| multistart |
También se proporciona un script que ejecuta 1 iteración de cada algoritmo, sobre cada uno de los datasets, y guarda los resultados en una hoja de cálculo. Se puede ejecutar mediante el siguiente comando:
python src/execution.pyNota: se precisa instalar la biblioteca XlsxWriter para la exportación de los resultados a un archivo Excel.
Análisis de los resultados
Enfriamiento simulado
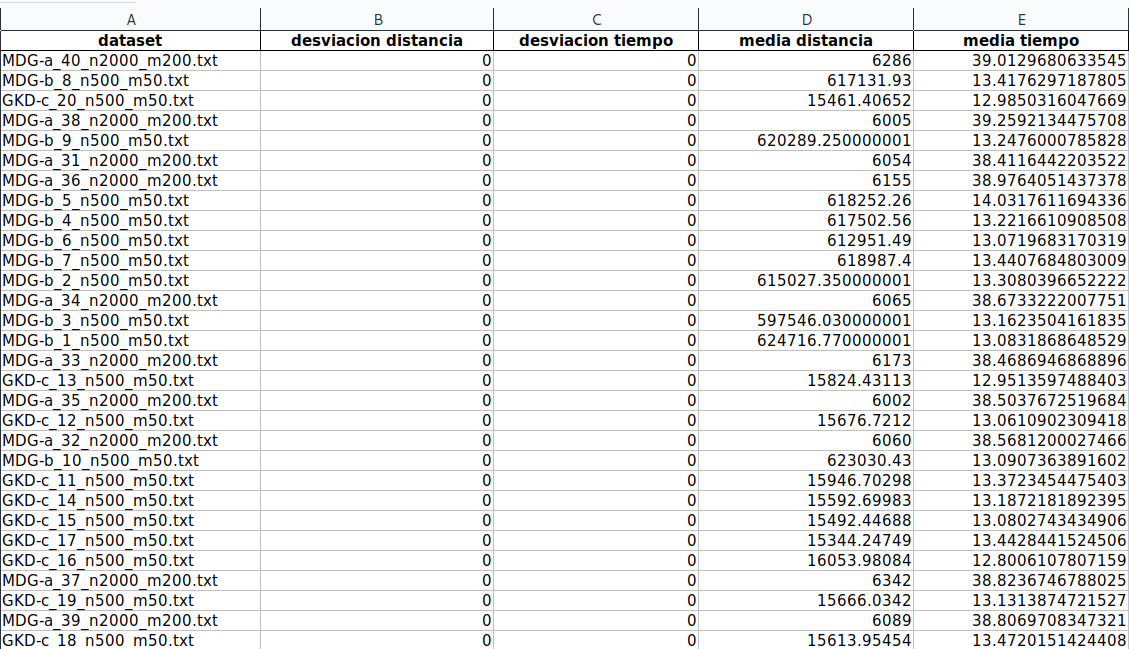
El tiempo de ejecución varía ligeramente según el dataset:
- Dataset con n=500: 13 segundos
- Dataset con n=2000: 38-39 segundos
La distancia total obtenida, toma valores muy diferentes según el dataset en el que se ejecuta.
Búsqueda multiarranque
Desafortunadamente, un bug en el script de ejecución ha hecho que la segunda pestaña de la hoja de cálculo únicamente tenga el valor de los datasets.