5.4 KiB
Práctica 1
Práctica 1
Introducción
En esta práctica, usaremos distintos algoritmos de búsqueda para resolver el problema de la máxima diversidad (MDP). Implementaremos:
- Algoritmo Greedy
- Algoritmo de búsqueda local
Algoritmos
Greedy
El algoritmo greedy añade de forma iterativa un punto, hasta conseguir una solución de tamaño m.
En primer lugar, seleccionamos el elemento más lejano de los demás (centroide), y lo añadimos en nuestro conjunto de elementos seleccionados. A éste, añadiremos en cada paso el elemento correspondiente según la medida del MaxMin. Ilustramos el algoritmo a continuación:
\begin{algorithm} \KwIn{A list $[a_i]$, $i=1, 2, \cdots, m$, that contains the chosen point and the distance} \KwOut{Processed list} $Sel = [\ ]$ $centroid \leftarrow getFurthestElement()$ \For{$i \leftarrow 0$ \KwTo $m$}{ \For{$element$ in $Sel$}{ $closestElements = [\ ]$ $closestPoint \leftarrow getClosestPoint(element)$ $closestElements.append(closestPoint)$ } $maximum \leftarrow max(closestElements)$ $Sel.append(maximum)$ } \KwRet{$Sel$} \end{algorithm}Búsqueda local
El algoritmo de búsqueda local selecciona una solución aleatoria, de tamaño m, y explora durante un número máximo de iteraciones soluciones vecinas.
Para mejorar la eficiencia del algoritmo, usamos la heurística del primer mejor (selección de la primera solución vecina que mejora la actual). Ilustramos el algoritmo a continuación:
\begin{algorithm} \KwIn{A list $[a_i]$, $i=1, 2, \cdots, m$, the solution} \KwOut{Processed list} $Solutions = [\ ]$ $firstSolution \leftarrow getRandomSolution()$ $Solutions.append(firstSolution)$ $lastSolution \leftarrow getLastElement(neighbour)$ $maxIterations \leftarrow 1000$ \For{$i \leftarrow 0$ \KwTo $maxIterations$}{ \While{$neighbour \leq lastSolution$}{ $neighbour \leftarrow getNeighbouringSolution(lastSolution)$ $Solutions.append(neighbour)$ $lastSolution \leftarrow getLastElement(neighbour)$ } $finalSolution \leftarrow getLastElement(Solutions)$ } \KwRet{$finalSolution$} \end{algorithm}Implementación
La práctica ha sido implementada en Python, usando las siguientes bibliotecas:
- NumPy
- Pandas
Instalación
Para ejecutar el programa es preciso instalar Python, junto con las bibliotecas Pandas y NumPy.
Se proporciona el archivo shell.nix para facilitar la instalación de las dependencias, con el gestor de paquetes Nix. Tras instalar la herramienta Nix, únicamente habría que ejecutar el siguiente comando en la raíz del proyecto:
nix-shellEjecución
La ejecución del programa se realiza mediante el siguiente comando:
python src/main.py <dataset> <algoritmo>Los parámetros posibles son:
| dataset | algoritmo |
| Cualquier archivo de la carpeta data | greedy |
| local |
También se proporciona un script que ejecuta 1 iteración del algoritmo greedy y 3 iteraciones de la búsqueda local, con cada uno de los datasets, y guarda los resultados en una hoja de cálculo. Se puede ejecutar mediante el siguiente comando:
python src/execution.pyNota: se precisa instalar la biblioteca XlsxWriter para la exportación de los resultados a un archivo Excel.
Análisis de los resultados
Los resultados obtenidos se encuentran en el archivo algorithm-results.xlsx, procedemos a analizar cada algoritmo por separado.
Algoritmo greedy
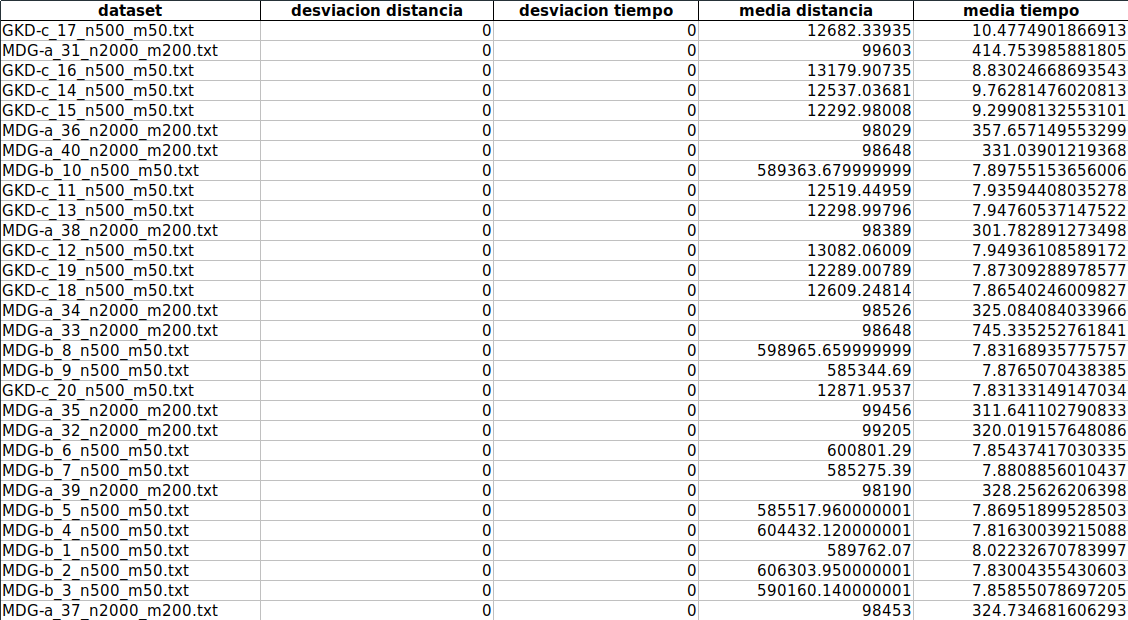
El algoritmo greedy es determinista, por lo tanto la desviación típica es nula, dado que se ejecuta una única vez. El tiempo de ejecución varía considerablemente según el dataset:
- Dataset con n=500: 7-10 segundos
- Dataset con n=2000: 5-12 minutos
La distancia total obtenida, por lo general, es inferior al algoritmo de búsqueda local, aunque no difiere significativamente.
Algoritmo de búsqueda local
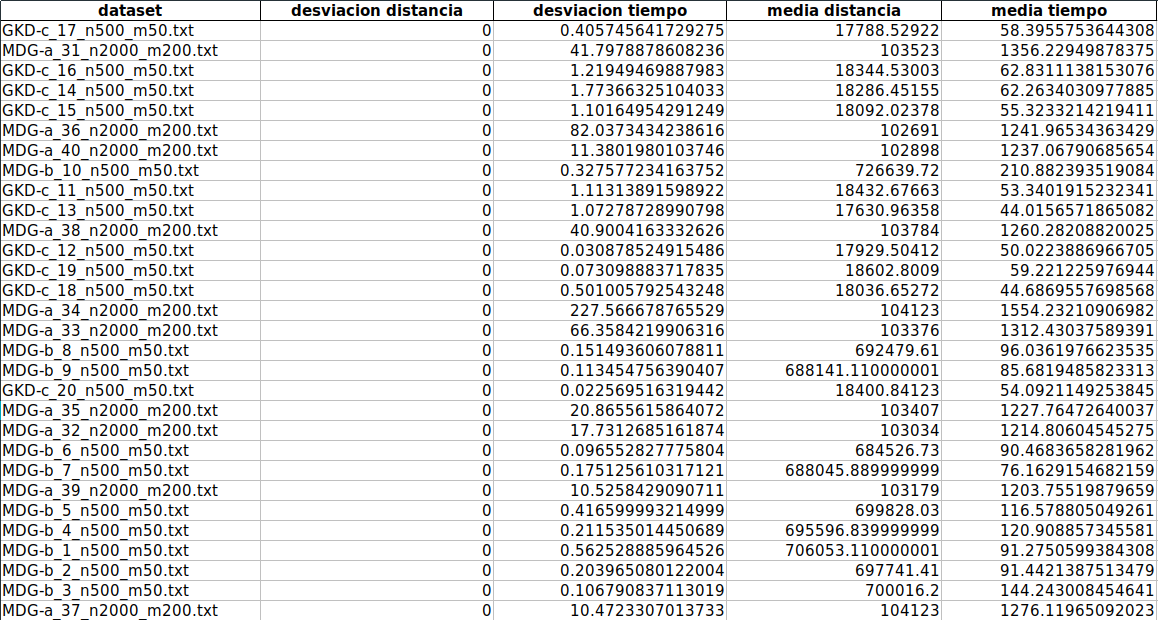
El algoritmo de búsqueda local es estocástico, debido a que para la obtención de cada una de las soluciones se utiliza un generador de números pseudoaleatorio. El tiempo de ejecución varía considerablemente según el dataset:
- Dataset con n=500: 1-2 minutos
- Dataset con n=2000: 20-25 minutos
La distancia total obtenida, por lo general, es superior al algoritmo greedy lo cual indica que la búsqueda local obtiene mejores resultados a expensas del tiempo de ejecución.
Debido a nuestras limitaciones computacionales, las ejecuciones de este algoritmo se hicieron con 100 iteraciones máximas.